
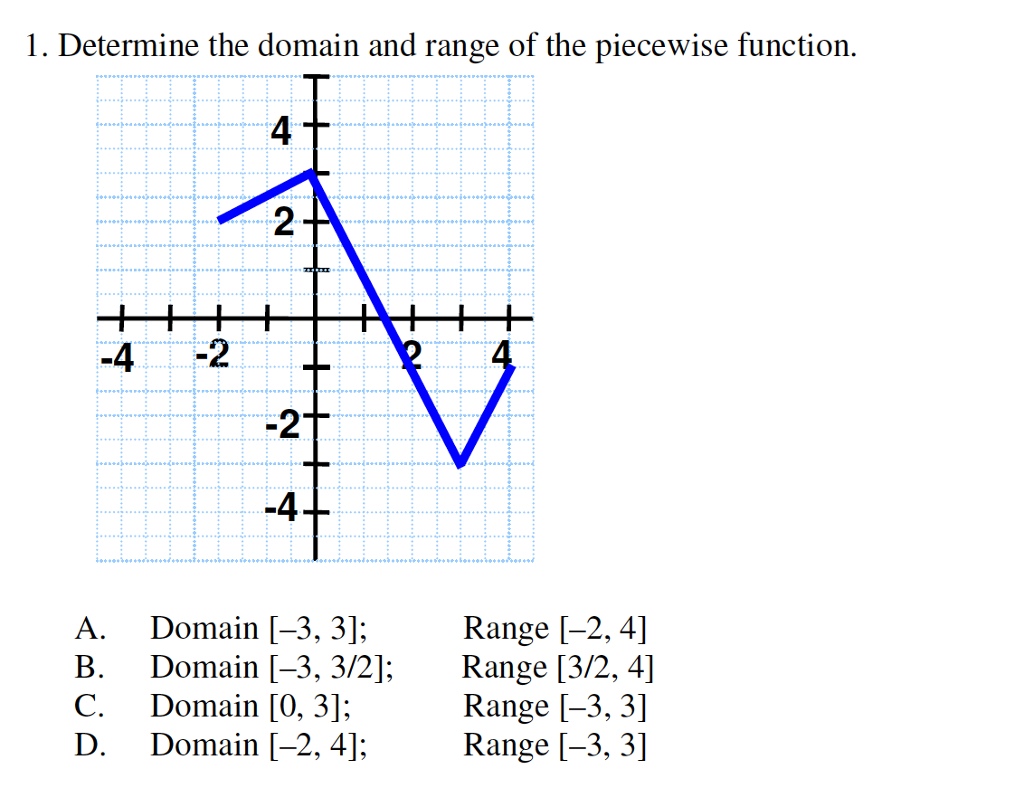
Is always going to be greater than that, as well it's going to be This doesn't actually include 4, but as we approach for, we could say, OK, 1 negative 4 is negative 3 so that's, so g of x So if you take the upper end, even though To you because it can be little bit confusing because this takes on its minimum value when x is approaching, or it'sĪpproaching its minimum value when x is approaching its, when x isĪpproaching its maximum because we're subtracting it. So as long as x is less than 4, then negative 3 is going to be less than g of x. So if x, let's see, if we said x was 4,Īlthough that's not this clause here, 1 minus x, 1 minus 4 is negative 3. It can't quite take on for, but it's going to approach for. Its smallest value when x is as large as possible. Now here we have 1 minus x, so this is going to take on X equals negative 3 in which case g of x actually That value because this is less than or equal to, so we can actually take on
#Domain and range of piecewise functions plus
So when x is equal to negative 3, negative 3 plus 7 is equal to 4, positive 4.
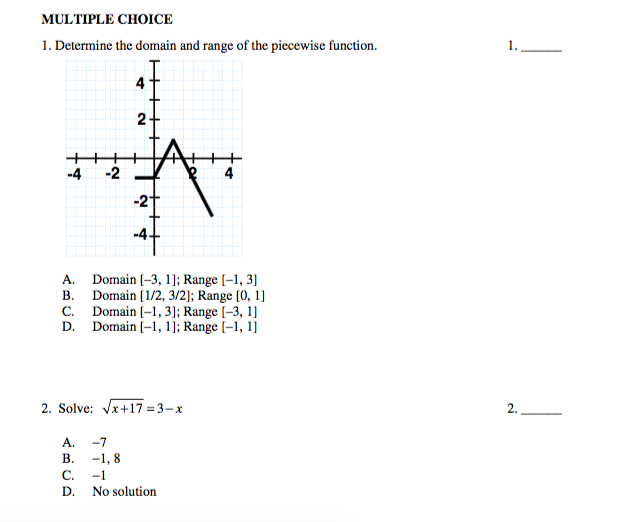
We can take on is x being equal to negative 3.

Into this, negative 6 plus 7 is equal to 1. And the reason I said that is if I put negative 6 To think about it is if negative 6 is less than x, then 1 is going to be less than g of x. So if x is greater than negative 6, g of x is going to be greater than 1, or another way
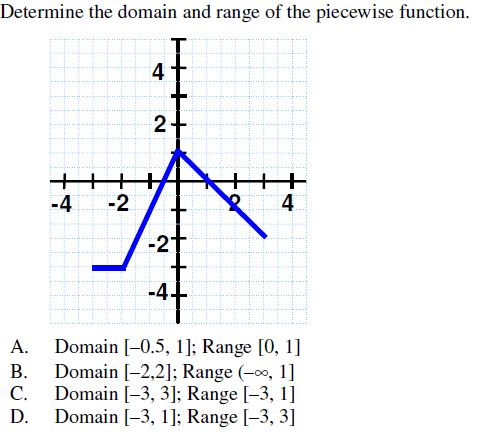
Would be equal to negative 6 plus 7, would be, would be 1. So if x were equal to negative 6, it can'tĮqual negative 6 herer but if x is equal to negative 6, then this thing over here Going to be as small as possible when x is approaching negative 6. Point? o this thing hits, hits its low point when x is as small as possible. What? And it might actually, this might be someĮqual signs there but I'm gonna worry about that in a second. What? g of x is going to be between what and To be between what and what? g of x is going to be between what and That g of x could take on? Let's think about that. And to do that, let's just think aboutĪs x goes, but x varies or x can be any values in this Outputs that this function can take on, or all the Is, this is the set of all inputs, oh sorry, this is the set of all Let's think about the range, and the range Now another way to say this and kind of less math-y notation is x, x can be any real number, any the real number such that, such that negative 6 is less than x is less than or equal to 6. So x at the high end is said to be less than As soon as we cross negative 3, we fall into this clause up to 4, butĪs soon as we get 4, we're in this clause up to and including 6. So as x goes, I just wanna make sure that we fill in all the gaps between x being a greater than negative 6 and Negative 6 is less than x and I also think about the upper bound. I could say x is a member of the real numbers such that, such that negative 6 is less than x. Let me write this way x, I could write it more math-y. Of our domain is defined right over there, so we say, we could say, negative 6 is less than x and I'm leaving. So this part right over here, the low end So, to fall into one of these three, you have And if x doesn't fall into one of those threeĬonditions, well this function g is just not defined. It is just saying, look, if x falls into one of these threeĬonditions, apply this. It doesn't say hey do this in all other cases for x. It doesn't, it doesn't fall into one of these three intervals. If it, if x is negative 6 or or lower than that. The domain is the set of all inputs for which this function is defined, and our input g of x is defined by a a line or the line changes depending Right over here for different intervals of x.


 0 kommentar(er)
0 kommentar(er)
